The fatigue performance of a metallic alloy is strongly influenced by its microstructure, especially in the crack nucleation regime. Micromechanics based fatigue modeling [1] is the appropriate tool to account for this influence. In this framework, fatigue life is obtained from a fatigue indicator parameter (FIP), function of the microscopic field values (plastic strain, stress, etc) obtained by the numerical simulation of a Representative Volume Element (RVE) of the microstructure (Figure below) subject to cyclic loading. The maximum FIP in a RVE determines its life (number of cycles N) through a phenomenological law calibrated with experiments (1)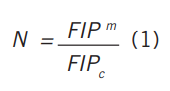
in which FIPc and m are the fitting parameters.
Although this framework has been successfully applied to predict fatigue life in many engineering alloys [1], it presents some limitations. Since fatigue life is triggered by the FIP value in the hottest point, the average life predicted is RVE size dependent and fatigue laws linking FIP with life are valid only for the particular RVE size used for calibration. Moreover, specimen or component size is not considered in the tool and the resulting predictions are not able to capture specimen size effects.
To this aim, first the cumulative probability distribution of the maximum FIP per RVE in a set of RVEs with size V0, CDF0 (FIP), is fitted to an extreme value distribution.
Then, this distribution is extrapolated to the actual size of the specimen/component under study, V1, using the weakest link theory as
The life prediction law (eq. 1), now adjusted using two experiments and the CDF corresponding to the specimen size of those tests, is finally used to obtain the life distribution as function of the FIP distribution CDF1. The life predictions of this new framework are RVE size independent and account for the effect of the specimen/component size. The result of this strategy is shown in the Figure below, where the methodology has been applied to an Inconel 718 alloy subjected to uniaxial strain controlled fatigue tests with different strain ranges Δε.
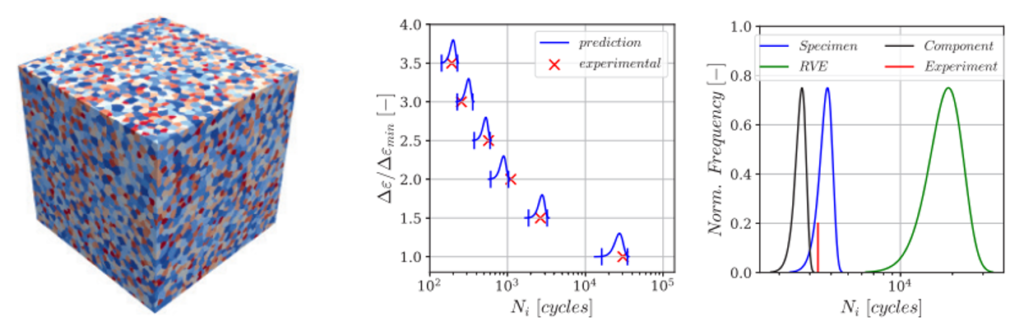
Left: Representative Volume Element (RVE) of a polycrystal with 40.000 grains for FFT homogenization. Right: Life prediction (Number of cycles for initiation) as function of the applied cyclic strain range, De. Right, life probability distribution for components of different sizes, small RVE size, typical specimen size and typical component size.
[1] Microstructure-sensitive computational modeling of fatigue crack formation
D. McDowell, F. Dunne
International Journal of Fatigue 32 (9), 1521-1542, 2010.
DOI: https://doi.org/10.1016/j.ijfatigue.2010.01.003
[2] An upscaling approach for micromechanics based fatigue: from RVEs to specimen and component life prediction
S. Lucarini, J. Segurado
International Journal of Fracture
DOI: https://doi.org/10.1007/s10704-019-00406-5
[3] On the accuracy of spectral solvers for micromechanics based fatigue modeling
S. Lucarini, J. Segurado
Computational Mechanics 63 (2), 365-382, 2019.
DOI: https://doi.org/10.1007/s00466-018-1598-1
